Bayes' theorem
An analysis of the problem using the formalism of Bayesian probability theory (Gill 2002) makes explicit the role of the assumptions underlying the problem. In Bayesian terms, probabilities are associated to propositions, and express a degree of belief in their truth, subject to whatever background information happens to be known. For this problem the background is the set of game rules, and the propositions of interest are:

: The car is behind Door i, for i equal to 1, 2 or 3.

: The host opens Door j after the player has picked Door i, for i and j equal to 1, 2 or 3.
For example,

denotes the proposition the car is behind Door 1, and
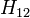
denotes the proposition the host opens Door 2 after the player has picked Door 1. Indicating the background information with

, the assumptions are formally stated as follows.
First, the car can be behind any door, and all doors are a priori equally likely to hide the car. In this context a priori means before the game is played, or before seeing the goat. Hence, the prior probability of a proposition

is:

Second, the host will always open a door that has no car behind it, chosen from among the two not picked by the player. If two such doors are available, each one is equally likely to be opened. This rule determines the conditional probability of a proposition

subject to where the car is — i.e., conditioned on a proposition

. Specifically, it is:

The problem can now be solved by scoring each strategy with its associated posterior probability of winning, that is with its probability subject to the host's opening of one of the doors. Without loss of generality, assume, by re-numbering the doors if necessary, that the player picks Door 1, and that the host then opens Door 3, revealing a goat. In other words, the host makes proposition H_{13}\, true.
The posterior probability of winning by not switching doors, subject to the game rules and H_{13}\,, is then P(C_1 | H_{13},\,I). Using Bayes' theorem this is expressed as:
By the assumptions stated above, the numerator of the right-hand side is:
The normalizing constant at the denominator can be evaluated by expanding it using the definitions of marginal probability and conditional probability:

Dividing the numerator by the normalizing constant yields:
Note that this is equal to the prior probability of the car's being behind the initially chosen door, meaning that the host's action has not contributed any novel information with regard to this eventuality. In fact, the following argument shows that the effect of the host's action consists entirely of redistributing the probabilities for the car's being behind either of the other two doors.
The probability of winning by switching the selection to Door 2,
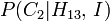
can be evaluated by requiring that the posterior probabilities of all the

propositions add to 1. That is:

There is no car behind Door 3, since the host opened it, so the last term must be zero. This can be proven using Bayes' theorem and the previous results:

Hence:

This shows that the winning strategy is to switch the selection to Door 2. It also makes clear that the host's showing of the goat behind Door 3 has the effect of transferring the 1/3 of winning probability a-priori associated with that door to the remaining unselected and unopened one, thus making it the most likely winning choice.
i cant be stuffed adding all the pictures, so get over it.

 : The car is behind Door i, for i equal to 1, 2 or 3.
: The car is behind Door i, for i equal to 1, 2 or 3. : The host opens Door j after the player has picked Door i, for i and j equal to 1, 2 or 3.
: The host opens Door j after the player has picked Door i, for i and j equal to 1, 2 or 3. denotes the proposition the car is behind Door 1, and
denotes the proposition the car is behind Door 1, and 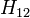 denotes the proposition the host opens Door 2 after the player has picked Door 1. Indicating the background information with
denotes the proposition the host opens Door 2 after the player has picked Door 1. Indicating the background information with  , the assumptions are formally stated as follows.
, the assumptions are formally stated as follows. is:
is:
 subject to where the car is — i.e., conditioned on a proposition
subject to where the car is — i.e., conditioned on a proposition  . Specifically, it is:
. Specifically, it is:

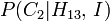 can be evaluated by requiring that the posterior probabilities of all the
can be evaluated by requiring that the posterior probabilities of all the  propositions add to 1. That is:
propositions add to 1. That is:

